الحصة (3)/ العلاقات الرياضية (التناسب)

 

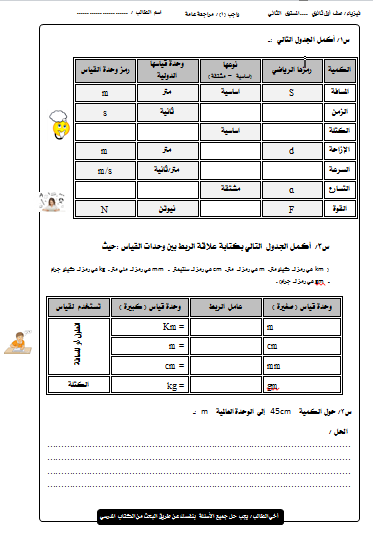
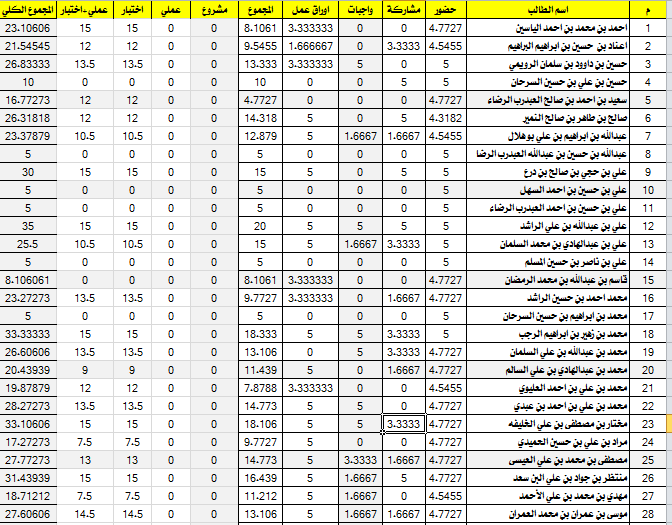
التناسب

التناسب عبارةٌ عن مقارنةٍ رياضيةٍ بين رقمين، وفي كثيرٍ من الأحيان يمكن أن تُمثل هذه الأرقام مقارنةً بين الأشياء أو الأشخاص. على سبيل المثال، دخلت غرفةً مليئةً بالأشخاص وتريد أن تعرف عدد الأولاد هناك مقارنة بعدد الفتيات في الغرفة، تُكتب هذه المقارنة في شكل نسبةٍ، تدعى بالتناسب.

التناسب هو ببساطةٍ عبارة عن نسبتين (كسرين) متساويتين.

يرمز لكلمة التناسب (العلاقة ) بالرمز 

أنواع التناسب للتناسب أنواعٌ تُحدَّد حسب العلاقة بين المقدارين الذين تمت المقارنة بينهما، وتندرج هذه الأنواع فيما يأتي: 

1- التناسب الطردي: (Directly proportional) :-

هي العلاقة التي توصف بأن زيادة أحد المقدارين ترتبط بزيادة الآخر بقيمةٍ ثابتةٍ مرتبطةٍ بالمقدارين معاً، وتسمّى ثابت النسبة، فمثلاً إذا تناسب المقدار أ مع المقدار ب طردياً؛ فإن  أ = ك×ب؛ حيث: ك هو ثابت النسبة بين العددين. فعلى سبيل المثال إذا كانت أجرة أحد العمال مقابل ساعة عمل واحدة تساوي 5 دنانير، فإن العلاقة التي تربط بين ساعات عمله وأجرته طردية؛ فكلما زادت ساعات العمل زاد أجر العامل، أما بالنسبة لثابت النسبة الذي يربط بين المقدارين فهو العدد 5؛ أي أن الأجر يتضاعف بمقدار 5 في كل مرة يزداد فيها عمل العامل ساعة واحدة، أما بالنسبة لمقدار ما يتقاضى هذا العامل من المال عند العمل لمدة 8 ساعاتٍ متواصلة فهو: الأجر= ثابت النسبة × عدد ساعات العمل= 5 ×8 ساعات= 40 دينار، وهو المبلغ الذي يتقاضاه العامل مقابل 8 ساعات من العمل.

كيف نميز رياضياَ العلاقة (التناسب ) الطردية بين متغيرين؟

إذا كان كلا المتغيرين في البسط أو كلاهما في المقام وبشرط بينهما علامة يساوي (=) .

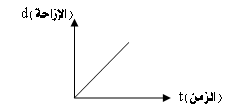
كيف نميز بيانياً بالرسم  العلاقة(التناسب )  الطردية ؟

عندما يكون شكل المنحنى بين المتغيرين كما في الرسم .

 2-التناسب العكسي: (Inversely proportional) :-

هي العلاقةٌ التي توصف بأن زيادة أحد مقداري النسبة يرتبط بانخفاض الآخر بقيمة ثابتةٍ مرتبطةٍ بالمقدارين معاً، وتسمى ثابت النسبة؛ فمثلاً إذا تناسب المقدار أ مع المقدار ب عكسياً؛ فإن: أ = ك/ب؛ حيث: ك هو ثابت النسبة بين العددين. ومن الأمثلة المتعددة على النسبة العكسية، نسبة سرعة سيارة إلى الزمن اللازم للوصول، فكلما زادت السرعة قلَّ الوقت اللازم للوصول، والعكس صحيح كذلك؛ فكلما قلت السرعة زاد الوقت اللازم للوصول، وإذا قام 4 عمالٍ مثلاً ببناء حاجزٍ ما، واستغرق بناؤه 3 ساعاتٍ، فإن العلاقة التي تربط بين عدد العمال والزمن اللازم لإنهاء العمل هي علاقة عكسية، فكلما زاد عدد العمال قلَّ الوقت اللازم لإنهاء العمل، لأن زيادتهم تؤدي إلى إنجاز العمل بشكلٍ أسرع وبأقل وقت، أما بالنسبة لثابت النسبة فهو: 3 = ك/4، وبضرب طرفي المعادلة بالعدد 4، ينتج أن: ثابت النسبة = 3×4 = 12، ولو اقترضنا أن عدد العمال أصبح 6 فإن الوقت اللازم لإنهاء العمل هو: ثابت التناسب÷عدد العمال= الوقت اللازم لإنهاء العمل، ومنه: 12/6= 2 ساعة؛ إذن الوقت الذي نحتاجه لإنهاء العمل إذا كان عدد العمال 6 هو ساعتان فقط. 

كيف نميز رياضياَ العلاقة (التناسب ) العكسية بين متغيرين؟

إذا كان أجد المتغيرين في البسط أوالآخر في المقام وبشرط بينهما علامة يساوي (=) .

كيف نميز بيانياً بالرسم  العلاقة (التناسب ) العكسية؟

عندما يكون شكل المنحنى بين المتغيرين كما في الرسم .

3-التناسب الأُسي: هي علاقةٌ أُسيةٌ تربط بين مقداري النسبة؛ بحيث إن المقدار الأول يساوي المقدار الثاني مرفوعاً إلى أُس من الرتبة الثانية، أو الثالثة، أو غير ذلك، ومضروباً بقيمة معينة هي ثابت النسبة؛ فمثلاً إذا تناسب المقدار أ مع المقدار ب أسياً؛ فإن: أ = ك×ب ن؛ حيث: ك هو ثابت النسبة بين العددين، ن: الأس من الرتبة الثانية أو الثالثة أو غيرها.فمثلاً لو تم إسقاط كرةٍ من سطح عمارةٍ، وكانت المسافة التي تقطعها الكرة تتناسب مع مربع وقت السقوط على النحو الآتي: المسافة = ثابت النسبة×مربع الزمن، فإذا علمنا أن الكرة قد قطعت مسافة 19.6م بعد ثانيتين من سقوطها فإن ثابت النسبة هو:

 المسافة التي قطعتها الكرة = (الزمن)²× ثابت النسبة

 وعليه: 19.6م = 2²×ثابت النسبة،

 ومنه: ثابت النسبة = 4.9

 أما المسافة المقطوعة بعد مرور ثلاث ثوانٍ فهي: 

المسافة المقطوعة= 4.9×3² = 44.1م

 بعض استخدامات النسبة والتناسب :-

يمكن استخدام النسبة والتناسب في حالة الرغبة بمضاعفة الكميات أو المقادير أو تقليلها مثلاً؛ وذلك عن طريق ضرب النسب أو قسمتها على العدد نفسه؛ فمثلاً لو أردنا عمل وصفةٍ لفطيرة ما تحتاج إلى 2 أكوابٍ من الزيت، و3 كوب من الطّحين، فإن النسبة بين الطحين إلى الزيت فيها هي 2:3، وإذا احتجنا إلى مضاعفة الكمية أربع مرات حتى تكفي لعدد أكبر من الأشخاص فإن الأمر يتطلب ضرب القيم في النسبة بالعدد (4)، لتصبح الكمية المطلوبة هي 12 كوب من الطحين، و 8 أكواب من الزيت؛ أي أن النسبة الجديدة ين الطحين إلى الزيت هي: 8:12، والامر نفسه ينطبق على تقليل الكمية. تُستخدم النسبة والتناسب أيضاً في المقاييس المختلفة عند رسم الخرائط والصور؛ فمثلاً إذا أردنا رسم العلم مثلاً؛ فإنه يمكن مضاعفة حجمه وتكبيره أو تصغيره عن طريق معرفة النسبة بين طوله وعرضه؛ فمثلاً إذا كانت النسبة بين طول العلم إلى عرضه هي: 2:3؛ وأردنا رسم علم طوله 20 إنش فيجب لعرضه وفق النسبة السابقة أن يكون 30 إنش؛ أي مضاعفة حجم العلم 10 مرات. يمكن كذلك استخدام النسب لمقارنة جزء إلى جزء، أو جزء إلى كل؛ فمثلاً يمكن كتابة نسبة عدد الذكور إلى الإناث في إحدى الغرف، أو كتابة نسبة عدد الإناث إلى العدد الكلي.